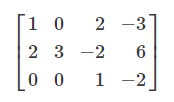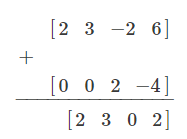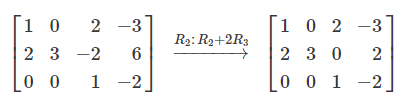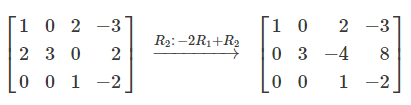Row vs. Column Operations

Before we explore the advantages of row operations, let's clarify these terms. Row operations pertain to altering the rows of a matrix, while column operations involve adjusting the columns. Here are the three fundamental row operations that can be performed on a matrix:

1. Interchanging Two Rows: This operation swaps the positions of two rows within a matrix.

   

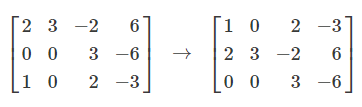
In the example above, Row 1 is exchanged with Row 2, and Row 2 is swapped with Row 3. The goal is to position element a11 in the top left corner.

2. Multiplying a Row by a Non-Zero Scalar: This step involves multiplying all elements in a row by a non-zero scalar.

   

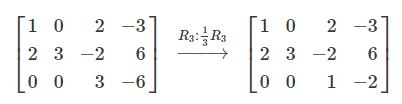
Here, Row 3 is multiplied by 1/3, yielding the desired 1 in Row 3, Column 3.

3. Adding a Multiple of One Row to Another: This operation adds a scalar multiple of one row to another row in the matrix.

We start with the matrix:

Instead of simply adding Row 2 to Row 3, we add Row 2 + (2 × Row 3):

We then replace Row 2 with the result:

This technique allows us to achieve a zero in Row 2, Column 3. We can repeat similar steps to eliminate other entries, ultimately leading to the 3 × 3 identity matrix on the left, thus solving the system.

The final steps involve additional row operations to achieve zeros in specific columns.

Row operations preserve the matrix structure, with rows still representing equations and columns representing variables. In contrast, column operations can alter the matrix's structure, complicating interpretation.

Benefits of Row Operations

Alignment with Mathematical Notation: One significant advantage of row operations is their consistency with conventional mathematical notation. When matrices represent systems of linear equations, rows correspond to equations and columns to variables, facilitating easier interpretation of results.

Ease of Execution: Row operations are generally simpler to perform, as they involve modifying one row at a time, making it easier to track changes. Conversely, column operations necessitate simultaneous manipulation of multiple columns, which can be more complex.

Maintaining Matrix Structure: Row operations maintain the integrity of the matrix structure, ensuring that rows still reflect equations in the system while columns represent variables. Column operations, however, can obscure this relationship by modifying column arrangements.

Applications of Row Operations

1. Solving Systems of Linear Equations: Row operations are crucial for solving linear equations. By applying these operations to a matrix, it can be transformed into a more manageable equivalent, leading to efficient and accurate solutions.

2. Matrix Inversion: Row operations can also be employed to compute the inverse of a matrix. By augmenting a matrix with the identity matrix and applying row operations, the inverse can be derived.

   

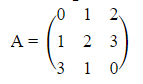
The steps involve multiple operations to achieve the desired inverse.

3. Eigenvalue Calculation: Row operations can assist in calculating a matrix's eigenvalues. By manipulating a matrix subtracted by a scalar multiple of the identity matrix, one can derive a polynomial equation whose roots correspond to the eigenvalues of the original matrix.

In summary, row operations prove to be more effective than column operations for matrix manipulation. Their alignment with standard mathematical notation, ease of execution, and preservation of matrix structure make them invaluable. Using row operations, one can solve linear systems, find matrix inverses, and conduct various matrix-related tasks.

Thank you for engaging with this exploration of matrix manipulation. Your interest represents a valuable contribution to the mathematical community, and I look forward to sharing more insights with you.