Chapter 1: Understanding the Concept

In this section, we delve into the question: what is the smallest number that can be evenly divided by the first twenty integers? To approach this, it's helpful to examine a simpler scenario first.

For instance, let's determine the least number that can be divided by the first four integers. The product of 1, 2, 3, and 4 yields 24. While 24 is divisible by these four numbers, it is not the minimal solution. In fact, 12 is the smallest number that meets this criterion, as it is also divisible by 1, 2, 3, and 4.

This discrepancy arises because 4 encompasses 2 in its multiplication, thus the contribution of 2 is redundant when calculating the least common multiple.

To extend this logic to find the smallest number divisible by the first twenty integers, we identify the highest power of 2 that divides a number less than or equal to 20, which is 16, expressed as 2⁴.

If we simply multiply all integers from 1 to 20, we would get a number divisible by 2⁵, but we only need 2⁴.

The Strategy

This method is applicable for any set of numbers from 1 to n, but we will specifically examine the case of 1 to 20.

Step 1: For each prime number, we will consider increasing powers until the next power exceeds 20.

Starting with 2:

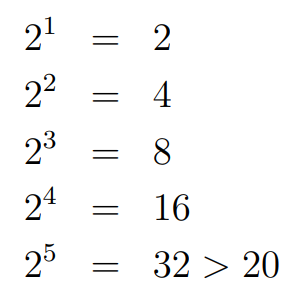
We will stop at 4, which we will record for future calculations.

Current numbers: {2⁴}.

Next, we analyze 3:

We halt at 2 here as well. Update our list:

Current numbers: {2⁴, 3²}.

Continuing with 5, since 5² equals 25, which exceeds 20, we will only include 5:

Current numbers: {2⁴, 3², 5}.

This pattern continues for all primes up to 20, resulting in:

Current numbers: {2⁴, 3², 5, 7, 11, 13, 17, 19}.

Step 2: We multiply these selected numbers together to find the smallest number divisible by all integers from 1 to 20:

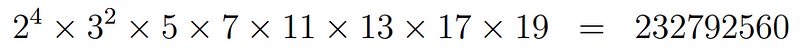
Now, with a solid method established, we can apply this to other examples. For instance, when examining the first fifteen numbers, we gather:

{2³, 3², 5, 7, 11, 13}, leading us to the smallest number divisible by integers 1 to 15.

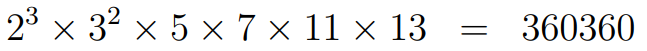
Similarly, the smallest number that is divisible by the integers from 1 to 100 can be calculated.

As a challenge, try to determine the smallest number that is divisible by all integers from 1 to 10.

Chapter 2: Video Explanations

To enhance your understanding of these concepts, here are two informative videos:

This video explains the least common multiple (LCM) of numbers from 1 to 20, providing a step-by-step approach.

In this video, discover how to find the least number that is divisible by all integers from 1 to 10, including practical examples.