Chapter 1: Understanding the Factorial Challenge

In this article, we delve into a more recent problem related to number theory, focusing specifically on factorials. While this problem is somewhat easier than others encountered, it still requires thoughtful consideration! Before checking the solution, give the problem a try yourself!

To simplify our discussion, let's clarify some notation: we say that a divides b (written as a | b) if the result of b/a is an integer.

Now, consider a divisor of k!, which we will denote as d. Given that d | k!m!, we can conclude that d also divides (k! + m!). Since we know that d divides k!, it follows that d must also divide m!.

What does this imply for us? We can indeed set d equal to k!, as our choice of d was arbitrary. Consequently, we arrive at the conclusion that k! | m!, indicating that we can express m! as j(k!) for some integer j, since k! must be a multiple of m!. Rearranging gives us:

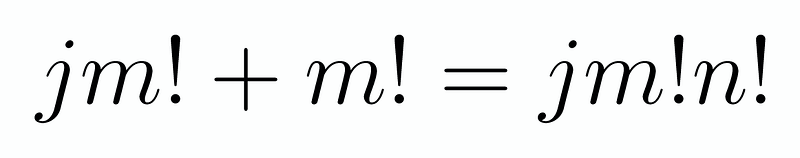
By canceling out the m! terms, we are left with a straightforward equation:

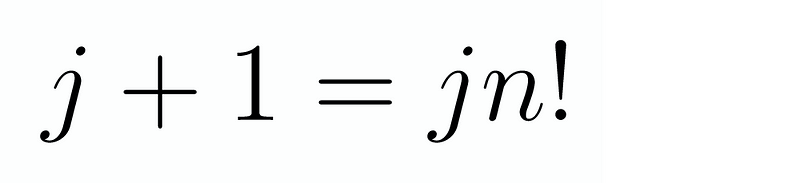
Finally, rearranging leads us to:

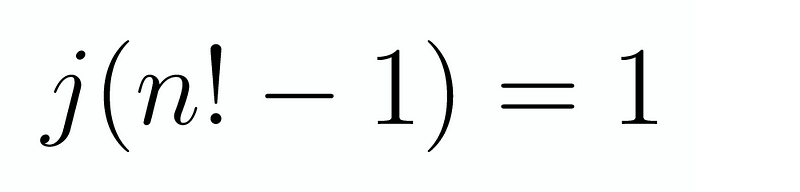
The only way this holds true is if j = 1 and n! - 1 = 1, which implies k = m and n! = 2, resulting in n = 2. Thus, our solutions are:

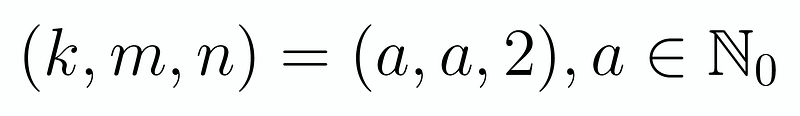
It's important to note that 0! equals 1!, giving us additional solutions:

Keep in mind that the factorial function, even when analytically extended, is not defined for negative integers, so we didn't need to consider those cases from the start.

However, there’s one more set of solutions we may have overlooked. For n ≥ 3, we can also express (n! - 2, n! - 1, n) since we can factor the left-hand side, leading to a valid solution. Readers should ponder why there are no further solutions beyond these.

Enjoyed this exploration? If you have suggestions for problems or articles, consider supporting us here! Your contributions are greatly appreciated!

Chapter 2: Engaging with Factorial Challenges

Discover more insights about factorials in the first video: Nice Factorial Equation - Can You Solve It? This video challenges you to think critically about a factorial problem.

The second video, A Great Factorial Question | 2024 Math Contest, further examines the nuances of factorial problems and offers additional perspectives.