Exploring the Existence of Magnetic Monopoles through Geometry
Written on
Understanding the Role of Geometry in Magnetic Monopoles
In this article, I aim to explore how the geometry of various spaces can influence the existence of certain physical entities. Specifically, I will focus on how magnetic monopoles can be realized within appropriate geometric frameworks. In classical electromagnetism, we rely on Maxwell's equations to determine the feasibility of different phenomena. Due to the nature of the divergence of magnetic fields being strictly zero, the existence of magnetic monopoles is deemed impossible.
To clarify, the divergence of a magnetic field is calculated by summing the partial derivatives of the field components in their respective dimensions.
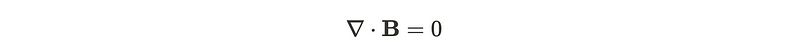
Why does this restriction exist? A magnetic monopole would necessitate a non-zero flux, functioning as a source. This can be demonstrated by analyzing the type of flux a monopole would emit. For a monopole to exist, it must act as a ‘source’, leading to a non-zero divergence in the field. Essentially, applying Stokes' theorem, we require:
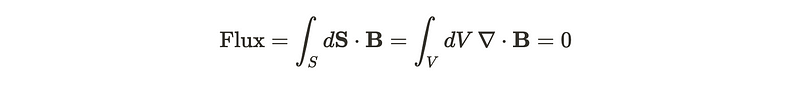
What causes the divergence of the magnetic field to be zero? This outcome is a mathematical property linked to how we can formulate the gauge potential. However, this rule can be bypassed if we consider non-standard topological constructs. To create such a monopole, we must explore a different spatial configuration. Instead of using the conventional Euclidean space R³, we can examine the space R³ — {0}. Topologically, this space is equivalent to a sphere embedded in three dimensions.
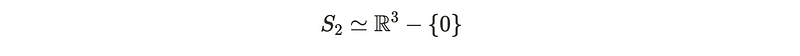
Linking Gauge Fields in Electromagnetism
Electromagnetism operates under the U(1) gauge symmetry, indicating that the physical framework remains consistent under certain transformations. The homotopy of our space corresponds to S², and our objective is to attach a U(1) bundle to this sphere. We can develop a non-trivial fiber bundle, which diverges from a simple cross product.

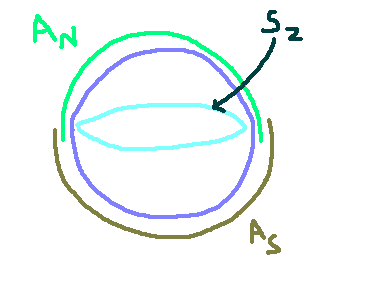
Constructing a non-trivial fiber bundle is feasible since S² is non-contractible. To achieve this, we define two distinct gauge fields across the Northern and Southern hemispheres. The surface of S² can be covered by two overlapping hemispheres, which we can connect by slightly extending their equatorial boundaries. Within the intersection, we can establish what we refer to as a transition function, which operates on the equator.
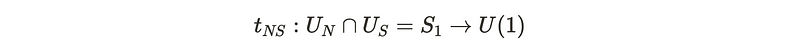
Within these sections, we can specify local gauge potentials. Following the Wu-Yang formalism, we need to select a set of gauge potentials that will also yield the magnetic monopole. After detailed calculations, it can be confirmed that the following gauge potential selection is valid:
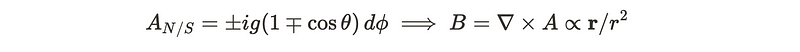
In the overlapping region, the gauge potentials are interconnected through a transition function, which must be well-defined to satisfy quantization conditions. Let tNS denote the transition function defined at the equator UN ∩ US. Thus, we require:
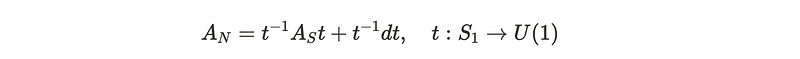
The transition function must adhere to a specific structure to be classified within U(1). This structure resembles a phase, similar to those applicable to wave functions. The relationship between the Northern and Southern hemispheres provides insights into constructing the precise form of the transition function. By substituting the vector potentials, we initially assume that the transition function is phase-based. Consequently, we determine that:
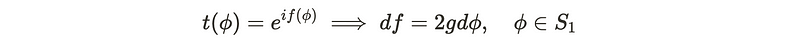
For t to be consistently defined, it must remain invariant under equivalence when φ is altered by multiples of 2π. This leads us to a quantization condition:
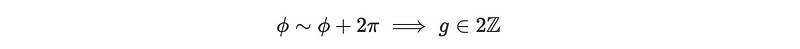
Exploring the Physics of Magnetic Monopoles
This insightful video by Felix Flicker delves into the intriguing concepts surrounding magnetic monopoles, providing a comprehensive overview of their theoretical foundations.
The Importance of Magnetic Monopoles in Physics
This video discusses the crucial arguments supporting the existence of magnetic monopoles and their implications within the realm of physics.