Exploring Matrix Differential Equations and Their Solutions
Written on
Chapter 1: Understanding Differential Equations
Many of you may have encountered differential equations or at least have some familiarity with the concept. These equations are vital in mathematics, and one of the most recognized examples is the Black-Scholes equation, which is essential for stock price modeling.
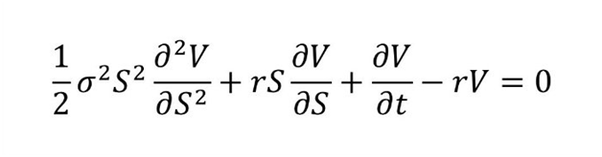
Today, we'll explore a specific type of differential equation that incorporates matrices. As we navigate through the solution, my aim is to provide clarity on how to approach new mathematical concepts while ensuring that each step is well-justified to cultivate a deeper understanding.
As we pursue the solution, we will examine two closely related methods for addressing this equation.
Section 1.1: The Equation and Its Components
To kick things off, we might feel inclined to multiply the matrices involved. However, that approach does not lead to a productive path. Instead, let us define ( A ) as our 2x2 matrix and represent ( r ) as our column vector to formulate:

This representation aids in deciding our approach, as it mirrors the structure of familiar differential equations. We have a constant matrix ( A ) alongside our dependent variable ( r ). If we overlook the presence of matrices and vectors, it becomes evident how we might solve this differential equation:
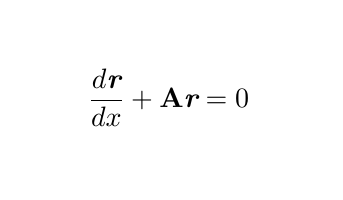
Assuming ( a ) is a constant, we have several methods to tackle this. A straightforward approach is to hypothesize the form of ( r ) in terms of ( x ), recognizing that the derivative of ( r ) is proportional to ( r ). This leads us to infer that the general form is ( r = C exp(lambda x) ). By substituting this expression into our equation and determining ( lambda ), we can find our constant ( C ) if initial conditions are provided.
Section 1.2: Applying the Approach
Now, let's apply this to our original differential equation. With sufficient motivation, we can explore this further. Readers may observe that our constants will ultimately be matrices, which we will clarify in our calculations.
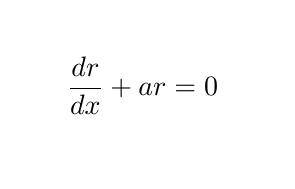
To satisfy the equation, we need ( M exp(lambda t) ) to not equal zero, thus leading us to conclude that ( lambda + A = 0 ).
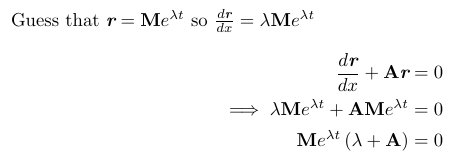
At this stage, one might wonder how exponentiation applies to matrices. It may appear complex, but let's recall the Maclaurin series for ( exp(x) ):
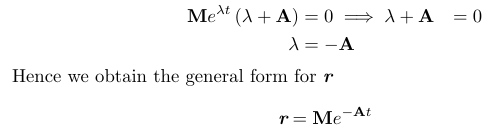
Traditionally, ( x ) is either a real or complex number. However, allowing ( x ) to be a matrix might seem unconventional. Regardless, let's proceed—there's no harm in trying!
To move forward, we must compute some powers of our matrix ( A ) for use in our series expansion.
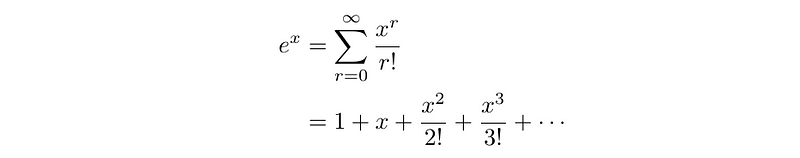
Now, we can substitute these powers of ( A ) into the Maclaurin series to see what results.
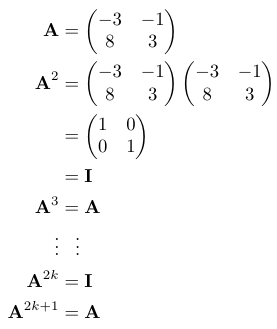
If you find this outcome as fulfilling as I do, you might be interested in further exploring the implications of exponentiating matrices. For more insight, check out my article on the intriguing results that arise from raising ( e ) to a matrix.
To determine our matrix ( M ), we must consider initial conditions satisfied by ( r ). Suppose we have the conditions:
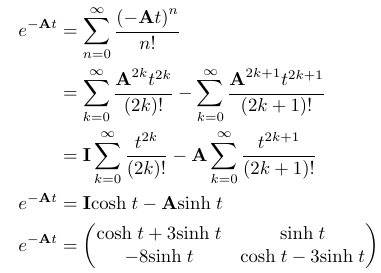
When we substitute these conditions into our expression for ( r ), we may encounter a challenge.
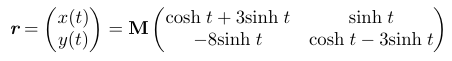
It is crucial to note that our matrix ( M ) must be positioned correctly to yield a valid multiplication outcome.
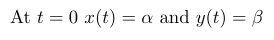
Ultimately, we can substitute ( M ) back into our expression for ( r ) to derive the solution to the differential equation.
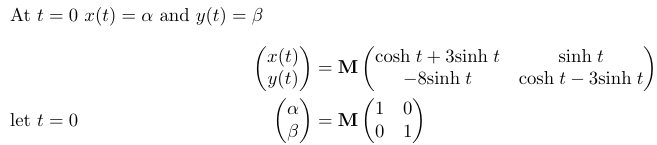
Chapter 2: Alternative Approaches to the Solution
Let's briefly explore another method for solving our differential equation, which also illustrates the significance of our matrix constant ( M ) on the right side of ( exp(-At) ).
Consider our differential equation once more:
To begin, we will find the integrating factor, which is defined as ( exp(P(x)) ), where ( P(x) ) is the function multiplying the dependent variable in the general form of the differential equation.

Here, our ( P(x) ) is simply the constant matrix ( A ).
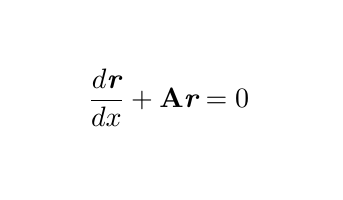
We need not concern ourselves with the integration constant while calculating the integral. This situation should feel familiar by now; let’s compute the integrating factor.
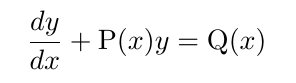
Next, we'll multiply our differential equation by this integrating factor, forming a 'perfect derivative,' while being cautious about the order of multiplication since matrix multiplication is not commutative.
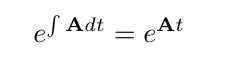
When we bring in ( exp(At) ), it’s necessary to pre-multiply by its inverse to maintain the correct multiplication sequence. This adjustment ensures that if ( M ) is a 2x1 matrix, we achieve the right dimensionality for ( r ).
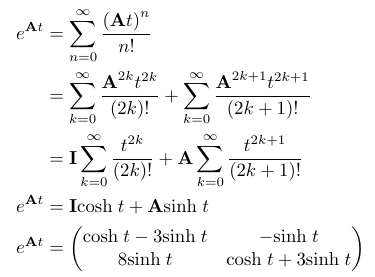
Consequently, we arrive at a familiar expression for ( r ) with the correct order of multiplication.

When we apply our initial conditions, we find the same matrix ( M ) as before.

Thus, we have effectively solved the differential equation using two distinct methods. I hope this exploration has broadened your understanding and demonstrated how to tackle unfamiliar challenges in mathematics.
Thank you for taking the time to read this. I welcome your thoughts and questions!