Exploring Inequalities from the Manchester Maths League Final
Written on
Chapter 1: Introduction to the Manchester Maths League
The Manchester Maths League Final took place just yesterday. Although this competition is relatively lesser-known and has only recently expanded beyond Manchester, it still presents intriguing problems. This year, participants from the northern regions of England qualified for the finals, with approximately 15 contenders. In this article, we will explore a specific inequality from this competition. Before diving into the solution, why not try tackling the problem yourself? You might surprise yourself with your skills!
Section 1.1: The AM-GM Inequality
Let’s begin by revisiting the AM-GM inequality, which states:

This may not seem directly relevant at this stage, but it's a crucial concept to remember as we work through the problem.
Section 1.2: Manipulating the Inequality
Notice that each fraction lacks one of the terms present in the other fractions on the left side. Therefore, it makes sense to multiply by the common factor of (a+1)(b+1)(c+1). This approach simplifies our calculations, avoiding the complexity often associated with cyclic inequalities. To eliminate the fraction on the opposite side, we will also multiply everything by 4. Consequently, we arrive at:
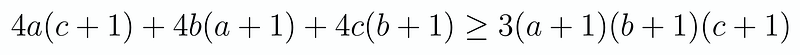
We can expand this expression conveniently and cancel out terms. Ultimately, we need to demonstrate the following:

This leaves us to prove that (a + b + c + ab + ac + bc leq 6) holds true. To remind you of our earlier assertion:
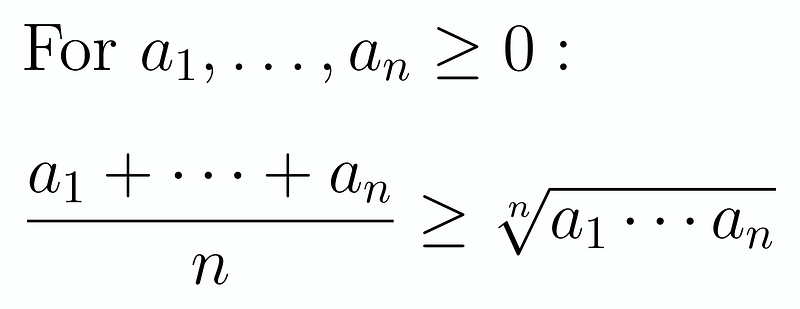
Indeed, these conditions are satisfied, confirming that:
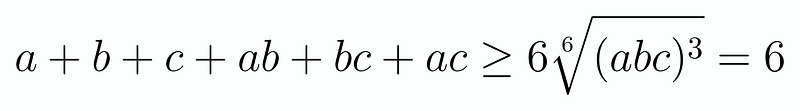
As required, we conclude that (abc = 1).