Chapter 1: Introduction to the Problem

I recently encountered an intriguing question from an old entrance exam at Cambridge designed for gifted high school students. This particular problem is crafted in a way that leads you to feel overly confident about its solution. However, there's a hidden twist that only those with a systematic and independent thought process are likely to uncover.

Before diving into the solution, I'll present the problem to give you a chance to solve it on your own.

The Problem

This question essentially revolves around determining the most efficient distance traveled along a curve. To tackle this challenge, it may be beneficial for you to familiarize yourself with the formula for calculating the length of an arc on a curve. I had to look this up as I had never encountered it before.

Chapter 2: Breaking Down the Road Length

To solve the problem, it’s helpful to sketch the scenario. Here’s my illustration that highlights the different segments of the road:

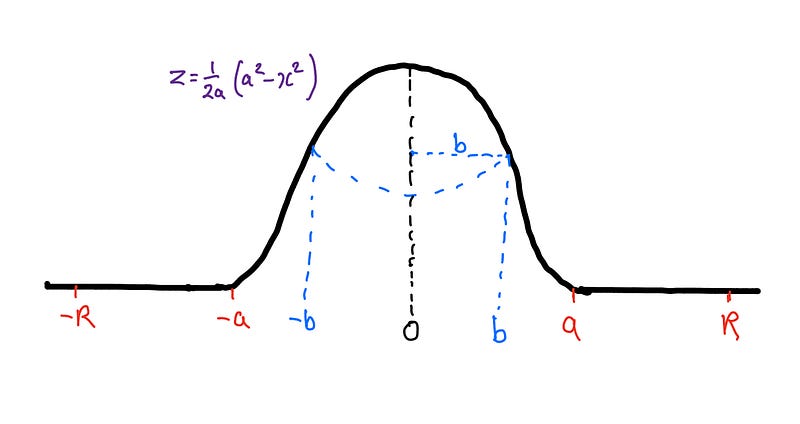
We can categorize the road into three segments:

1. Two straight, flat road sections between -R and -a, and between a and R, which together measure 2(R-a).
2. Two segments where the hill rises or falls, each matching the length of the arc of the parabolic curve from x = b to x = a.
3. The semicircular segment around the hill, representing half a circle with a radius of b, thus its length is (pi b).

The formula for the arc length of a curve (f(x)) from (x = b) to (x = a) is given by:

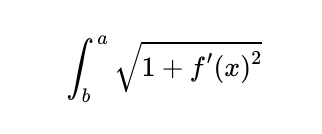
Here, (f'(x)) denotes the derivative of (f(x)) concerning (x). In this context, we have:

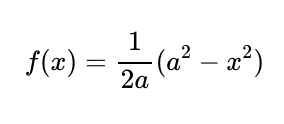
Combining all these segments, we can derive the formula for the total road length:

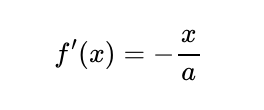
I've denoted this as (l(b)) since we aim to optimize the road length as a function of (b). Notably, I haven't performed the integration here, as it may be unnecessary for our purposes.

Chapter 3: Minimizing the Road Length

The task requires us to identify a value for (b) that minimizes the total road length (l(b)). To achieve this, we will differentiate (l(b)) with respect to (b) and solve for when the derivative equals zero.

This process involves differentiating an expression containing an integral, which effectively cancels out. Hence, integration in the earlier formula may not be needed. Let's formalize this approach.

Let:

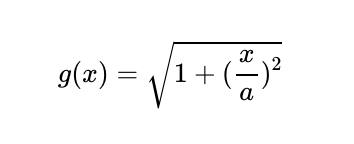
And define (G(x)) as a function such that (G'(x) = g(x)). Consequently, we can express:

By differentiating with respect to (b) and recognizing that terms not containing (b) vanish, we arrive at:

Setting this derivative to zero and solving for (b) yields:

At this point, one might think the problem is resolved. However, there’s a twist.

Chapter 4: The Unexpected Revelation

Let's analyze the expression we derived for (b). Given that (pi > 3), we deduce that (b > a). This contradicts our initial problem statement, indicating a flaw in our approach.

Revisiting the expression for the derivative of the road length:

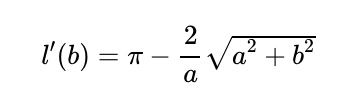
Considering values within the permissible range of (0 leq b leq a), we find that (pi > 2) and (pi > 2pi^2). Hence, we conclude that (l'(b) > 0) for all valid (b) values, indicating that (l(b)) is strictly increasing in this range. Therefore, the minimum length occurs at the boundary, specifically when (b = 0).

Thus, the optimal advice for the king is to go directly over the hill rather than navigating around it. Reflecting on the original question, I appreciate the subtle hints in parts (i) and (ii) that explicitly allow for (b = 0) as a feasible solution. I can imagine many aspiring mathematicians would easily fall for this clever trick.

What are your thoughts on this problem and my insights? I welcome your comments.

In the video titled "Deceptive Simplicity Unveiled: A Nice Exponential Equation with a Surprise Twist," you’ll discover how seemingly simple equations can reveal unexpected complexities in mathematical reasoning.

The second video, "Pythagoras Twisted Squares: Why Did They Not Teach You Any of This in School?" explores unconventional mathematical concepts that challenge traditional teachings.