Chapter 1: The Complexity of Pi Calculation

Calculating the nth digit of π (pi) after the decimal point without having to compute all preceding digits presents a formidable challenge. This area has witnessed remarkable advancements, notably with the introduction of the Bailey–Borwein–Plouffe (BBP) formula. Unveiled in 1995 by Simon Plouffe, this formula is named after David H. Bailey, Peter Borwein, and Simon Plouffe himself, who authored the foundational paper [1][2]. The emergence of the BBP formula was unexpected, as it was previously thought that determining the nth digit of π would be as complex as calculating the first n digits.

The BBP formula is groundbreaking because it enables the calculation of individual hexadecimal digits of π starting from any position, without the necessity of computing prior digits [1]. This represents a significant shift from conventional methods that generally require the computation of all preceding digits and often involve large data types to handle extensive numerical values.

The BBP formula is expressed as follows:

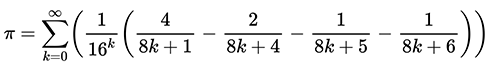
It can be adapted to compute hexadecimal or binary digits of π from an arbitrary starting point [1]. For instance, one can calculate ten hexadecimal digits of π beginning at the one millionth position in just a few seconds using modern computing power [4]. The BBP algorithm employs modular arithmetic, which ensures that only the fractional part of the sum remains when reducing modulo 8k + 1, facilitating the efficient calculation of:

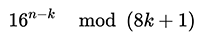
and allowing for the extraction of the desired digit [1].

While primarily used for hexadecimal extraction, the BBP formula has been adapted for binary digit extraction. However, it was not directly applicable to decimal digits [5]. Simon Plouffe later devised a method for calculating individual decimal digits of π without needing to compute preceding ones, although this approach is less efficient and impractical for determining digits further down the sequence [8]. The formula is characterized as a spigot algorithm, which generates digits sequentially, sometimes permitting the extraction of digits starting from any position [1][6].

The BBP formula and its variations have been employed in initiatives like PiHex, which calculated numerous digits of π through distributed computing. Furthermore, these formulas have been generalized to compute digits of other mathematical constants, such as log(2) and π². These digit-extraction algorithms are of particular interest as they contribute to the study of the normality of numbers, relating to how digits are distributed in their expansions [4][8].

Thus, BBP-type formulas have been discovered for various other irrational numbers, represented in general form as follows:

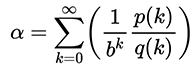
In these equations, π represents the irrational number being computed, while p(k) and q(k) are polynomials with integer coefficients, and b is an integer base [1]. However, a systematic method for determining the appropriate p(k), q(k), and b for a specific number π remains elusive.

Despite the BBP formula requiring less computational effort than traditional π-computing algorithms, it still operates with a linearithmic complexity of O(n log n). This implies that as n increases, so does the time needed to calculate the digit at that position [1].

Chapter 2: The Journey Behind the BBP Formula

The first video, "Scientists Just Discovered A New Formula For Pi Accidentally," delves into the unexpected origins of the BBP formula and its implications for the mathematical community.

The history of the BBP formula is a captivating narrative filled with discovery, collaboration, and controversy. Simon Plouffe's quest began with a desire to find a formula that could directly compute the digits of π. His partnership with notable mathematicians David Bailey and Peter Borwein culminated in the publication of the BBP formula. Yet, this story is not without its complications. Plouffe's account suggests that there were misattributions regarding contributions to the formula's discovery [7].

Initially, Plouffe, Bailey, and Borwein's collaboration appeared to be a successful blending of their mathematical prowess. However, tensions arose over the credit for the BBP formula, with Plouffe feeling his contributions were overshadowed by those of his collaborators. He expressed concern that Bailey received the majority of the credit, which Plouffe considered misleading. He clarified that the discovery of the formula was significantly aided by using programs like PARI-GP and Maple, which were crucial in the formula's development [3].

Continue reading the history as shared by Simon Plouffe in 2003…

Despite the controversies surrounding its development, the BBP formula represents a monumental achievement in mathematics. It has opened new avenues for calculating the digits of π and has inspired further investigations into BBP-type formulas for other constants.

Beyond its mathematical significance, the BBP formula underscores the importance of recognizing and correctly attributing contributions within collaborative research. Clear communication and acknowledgment of individual efforts in collective discoveries are essential, as illustrated in Simon Plouffe's experience.

The second video, "Can We Calculate 100 Digits of π by Hand? The William Shanks Method," explores historical methods of calculating π and compares them to modern advancements like the BBP formula.

The kn-one Conjecture: Fractal Signatures of Order Amidst Chaos

A Collatzian Journey of Mathematical Curiosity on Patterns, Predictability, and the Puzzles of Infinite Iterations

www.cantorsparadise.com

Sources

[2] Bailey, David H.; Borwein, Peter B.; Plouffe, Simon (1997). “On the Rapid Computation of Various Polylogarithmic Constants”. Mathematics of Computation. 66 (218): 903–913. doi:10.1090/S0025–5718–97–00856–9

[8] “Pick a Digit, Any Digit” http://mathtourist.blogspot.com/2020/09/pick-digit-any-digit.html?m=1