Chapter 1: Understanding de Sitter Spacetime

In a prior discussion, I delved into the derivation of the Einstein equations. Within the framework of general relativity, the primary focus is on the metric. These equations guide the evolution of the metric across space and time. When considering a vacuum devoid of mass or energy, the Einstein equations simplify considerably. They assert that the Ricci curvature tensor (which will be elaborated upon shortly) is proportional to the metric itself, with a scaling factor represented by the enigmatic ‘cosmological constant.’

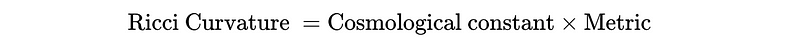
The Ricci curvature tensor serves as a broad measure of how a space deviates from the conventional flat or ‘Euclidean’ realm. It quantifies the deformation of a small volume as it follows its natural trajectory in spacetime. In mathematical notation, a capital R signifies the Ricci curvature tensor, appearing on the left side of the equation, while the cosmological constant is denoted by the Greek letter Lambda, and the metric is represented by the letter g.

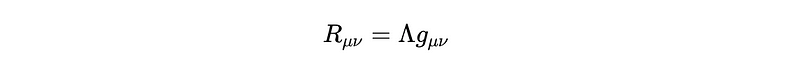
Let’s consider the scenario where the cosmological constant vanishes, i.e., ? = 0. In this case, we need to solve the equation R_µ? = 0. Although it might seem straightforward to assert g_µ? = 0, this is not permissible, as the metric necessitates an inverse. The requirement for the metric to maintain a non-zero determinant differentiates gravity from other field theories, leading us to the constraint that none of the eigenvalues can equal zero.

Interestingly, this condition implies the metric may not be a fundamental field. However, parallels can be drawn with fluid mechanics. For instance, the simplest solution to the Einstein equations, excluding the cosmological constant, is Minkowski spacetime, which can be illustrated in one time dimension and one spatial dimension as follows.

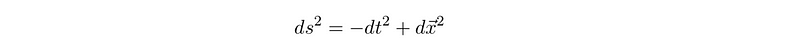
Exploring de Sitter Spacetime: The Initial Approach

Now, we encounter two distinctive cases based on the sign of the cosmological constant, either negative or positive. For a positive cosmological constant (i.e., ? > 0), we can seek solutions to the equation R = ?g. The range of possible solutions is extensive. To streamline the process, we will focus on those exhibiting spherical symmetry—solutions where the metric remains invariant across all angles. This assumption reduces our degrees of freedom, facilitating the search for a solution.

We posit that our metric is of the form below, incorporating a function f that we need to resolve. This function f correlates with both the radial and temporal components of the metric, while we apply the standard spherical metric for its angular characteristics.

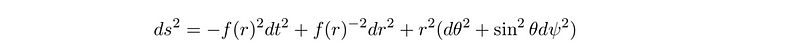
Determining the Function f

In the next steps, we will determine what the function f is. To achieve this, we will substitute our proposed ‘guess’ into the Einstein equations, yielding a specific equation for f that we can solve. Typically, this results in a differential equation.

To proceed, we will calculate our Ricci tensor R based on this metric ‘guess,’ leading to a rather intricate expression involving the function f. The mathematical derivation is laborious, so I’ve summarized the results for clarity. The Ricci tensor is a 2-rank tensor, meaning it has two indices and several components, which are detailed below.

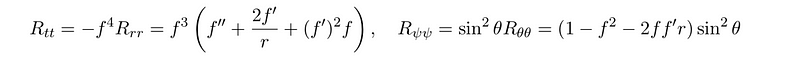
Using this ansatz, we can derive f(r) by setting R = ?g and solving the equation by substituting particular indices. For instance, by letting ?, ? = tt, rr, we obtain a second-order differential equation for the function f. This classification stems from the presence of a second-order derivative of f that we must account for.

Surprisingly, this equation is resolved by a relatively straightforward expression. Generally, mathematicians tackle such differential equations through computational methods or by making educated guesses and testing them.

To construct the complete metric, we must incorporate this function into our initial assumption. This substitution results in our final metric taking on a notably elegant form.

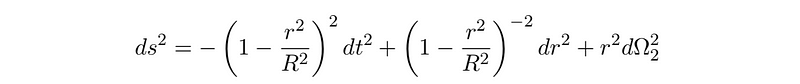
For brevity, we have condensed r²(d?² + sin2² ?d?²) into r² d?2², representing the square of the radius multiplied by the conventional metric on a unit 2-sphere. This simplification will prove beneficial in later calculations involving various parameterizations of this metric.

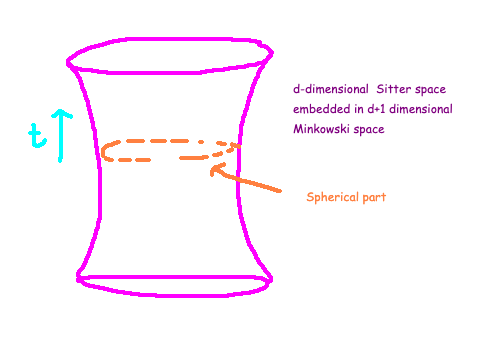
This depiction illustrates how de Sitter spacetime can be visualized as a hyperbolic section within a higher-dimensional Minkowski space. The metric we derived is referred to as de Sitter spacetime or the static patch of dS. It is important to note that we have a valid range from r ? [0, R], although the metric appears singular at r = R. In this segment, we will investigate whether this singularity arises from a poor choice of coordinates or represents a true physical spacetime singularity. It’s essential to remember that a coordinate singularity is permissible (as we will see, it indeed is), since coordinates are defined concerning coordinate patches.

Further Investigations

We can delve deeper into understanding this metric by examining geodesics. For instance, we can analyze the following action, where ? signifies proper time, and identify the geodesics that extremize this action, revealing the locations of our singularities.

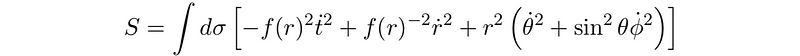
Additionally, we can explore various coordinate systems that describe the same metric. This exploration could provide insights into whether the singularity at r = R is a genuine metric feature. Lastly, physicists often embed de Sitter spacetime within higher-dimensional frameworks. I may elaborate on this in a future post.

Video Insights

To enhance your understanding of de Sitter spacetime, I recommend the following videos:

#### Gordon Belot: Ten Weird Things about de Sitter Spacetime

This lecture explores various intriguing aspects of de Sitter spacetime and its implications for cosmology.

#### Aspect of De Sitter Space (Lecture - 01) by Dionysios Anninos

In this lecture, the fundamental features of de Sitter space are discussed, providing a solid foundation for further exploration.

References