The Historical Significance of Knots

Knots have a rich and ancient history, with the earliest fossil evidence dating back around 30,000 years. They have played a vital role in various human activities, especially in sailing. Furthermore, knots have been prominently featured in art across different cultures, highlighting their pervasive presence in human civilization.

One of my favorite uses of knots comes from the Inca civilization in the Andes of South America. The Incas were remarkable for their innovative techniques; for example, they established an extensive road network throughout their vast empire without the wheel. They also developed a unique recording system called "Quipu," which consists of intricate strings and knots, serving an unknown record-keeping purpose. Clearly, knots are ubiquitous!

Given their significance in both technology and the arts, it was inevitable that mathematicians would explore knots further. Building on Gauss's notes, Lord Kelvin became interested in the potential links between knots and atomic structure. Along with physicist Peter Tait, he aimed to explain the arrangement of atoms through knot properties. They compiled a comprehensive list of knots, associating each with distinct atoms. Although this connection was later disproven with the advent of modern atomic theory in the early 1900s, their work established a foundation for a complex mathematical theory.

What Constitutes a Knot?

Mathematically, a knot can be visualized as a circle embedded in three-dimensional space. Two knots are considered identical if one can be transformed into the other without any cuts. Similar to rubber, knots can be reshaped into various forms. A key distinction is that mathematical knots are always closed, meaning they have no loose ends. The simplest knot is just a circle, but complexity increases significantly.

The number of crossings serves as a straightforward way to differentiate knots. However, one must be cautious! A circle can be crossed over itself multiple times in 3D space. Knot theorists focus on the minimum number of crossings for a knot. For instance, the notation “3?” indicates that this knot will always have at least three crossings, which cannot be reduced further. This knot is commonly known as the Trefoil Knot.

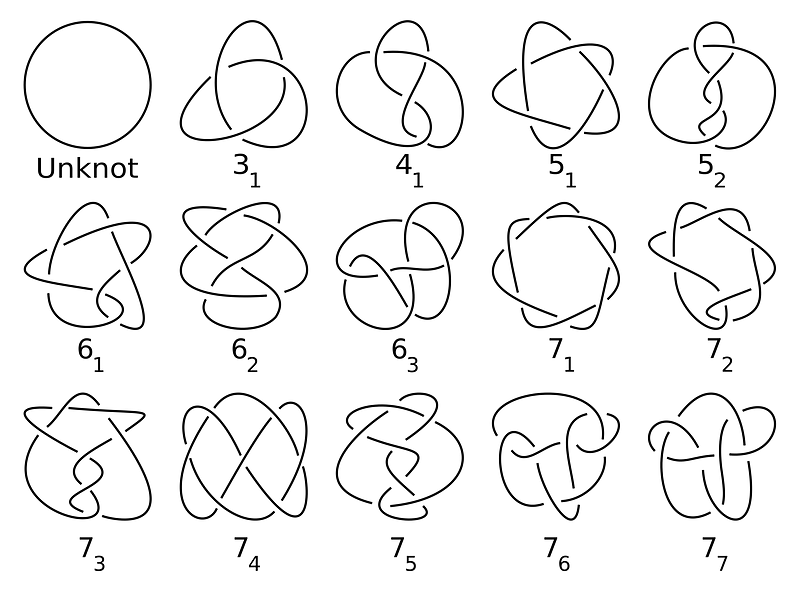
As the number of crossings increases, distinguishing between different knots becomes increasingly challenging. This challenge was highlighted in the 1970s when amateur mathematician Kenneth Perko discovered a mistake in a previously published table of knots with up to ten crossings. His observation that two knots, labeled as 10??? and 10??? respectively, were actually identical earned them the name "Perko Pair."

Knot theorists continually strive to differentiate knots, often using invariants—quantities that remain unchanged as the knot is manipulated. There are numerous invariants available; you can refer to this page for a list of various invariants related to knot 7?. However, challenges arise in ensuring that these invariants are unique for every distinct knot.

The Alexander Polynomial is perhaps the most well-known knot invariant. It offers a method to represent knots as polynomials with integer coefficients. For example, the Alexander Polynomial for the 3? knot is illustrated below.

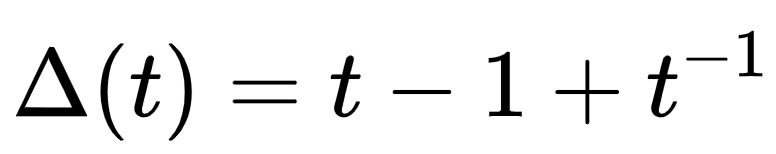
Nonetheless, it has been demonstrated that the Alexander Polynomial is not entirely reliable as an invariant, as there exist distinct knots that share the same polynomial. To address this limitation, various other polynomial mappings have been developed, including the Jones Polynomial and the HOMFLY Polynomial. Researchers in knot theory continue to devise innovative ways to classify knots.

The ongoing quest to list knots has led to a recent compilation that includes nearly 300 million knots up to 19 crossings. For more details about this list and the methodologies used in its creation, visit this page. Are we certain that no duplicates exist?

The Relevance of Knot Theory

As with any field of mathematics, the question of "why is this important?" naturally arises. While I believe mathematics is inherently beautiful and doesn’t require justification, knot theory offers a plethora of practical applications.

After the disproof of the connection between knots and atomic structures, knot theory remained largely a theoretical discipline for many years. Eventually, it began to find relevance in scientific fields, particularly in the study of DNA. Within cells, DNA undergoes constant copying and manipulation by various enzymes, often resulting in the formation of mathematical knots. Research has linked enzyme functions to the creation of specific knots.

Knot theory also plays a surprisingly significant role in statistical mechanics, a branch of physics. Modeling the behavior of individual molecules in a fluid is a complex task, and knots have become essential tools for simulating particle dynamics. While I won’t delve into the specifics here, I recommend checking out this insightful paper on the topic.

This article serves as an introductory glimpse into the captivating realm of knot theory; there remains a vast amount to learn! If you're interested in delving deeper, I highly recommend "The Knot Book," which provides an approachable yet in-depth exploration of knot theory and its applications. For a more rigorous examination, "An Introduction to Knot Theory" offers a graduate-level perspective on knots and their significance in topology. Additionally, for a comprehensive database of known knots, complete with visualizations and invariants, the Knot Atlas is an excellent resource.

I hope you found this information enlightening! If you enjoy my writing, consider becoming a Medium member through this link to support my work. Also, feel free to follow me for more articles on math and science, as I publish weekly.