Exploring the Enigma of Infinity in Mathematics
Written on
Chapter 1: The Fascination with Infinity
Infinity stands as one of the most captivating subjects in mathematics, yet it remains shrouded in mystery for many. While we often shy away from it, what if we chose to embrace it, to explore and comprehend its depths?

Photo by Yusuf Onuk on Unsplash
Mathematics has its roots in natural numbers, initially excluding zero. Although the concept of zero is now commonplace, it was once a radical idea. Our earliest interactions with mathematics involved counting, addition, and subtraction, all conducted with these "natural" numbers.
Zero, intriguingly, symbolizes nothingness. This definition might seem paradoxical: can a number signify “no number”? Today, we accept this without question.
A similar conundrum arises with infinity; it is not yet classified as a number. Notably, we can conceive of infinity by dividing any number by zero. Defining infinity as a number presents several challenges: it sometimes behaves like a number, at other times like multiple numbers, and occasionally is considered undefined. Moreover, we may encounter instances where one "infinite" quantity surpasses another.
There are likely more complexities at play.
Despite its elusive nature, mathematics has progressed from natural numbers to integers, incorporating zero and negative numbers, fractions, real numbers, complex numbers, and more recently, transfinite and p-adic numbers.

The concepts of transfinite and p-adic numbers are relatively new and often absent from standard number set diagrams. While the number sets depicted above focus on finite quantities, transfinite and p-adic numbers engage with infinity, providing critical insights into its nature.
Philosophical Dilemmas
Infinity has long posed questions not only in mathematics but also in philosophy. From Zeno's paradox to Gödel's incompleteness theorems, we grapple with profound inquiries.
Zeno’s Paradox of Achilles and the Tortoise
Can we continually subdivide a distance until we reach a discrete atomic unit? In nature, it occasionally seems possible to uncover the smallest segment of something, but does this hold universally? What if the process of subdivision is endless?
Zeno's paradox suggests that we can infinitely halve space, leading to the conclusion that a finite distance can be expressed as the infinite sum of finite components.
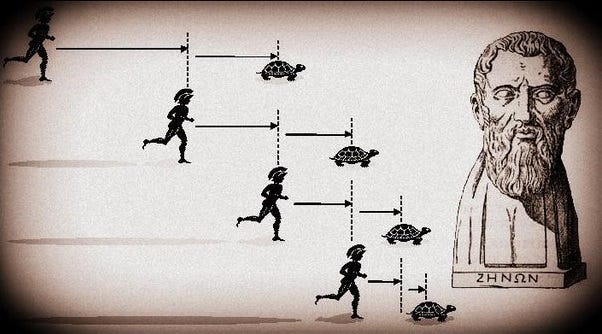
We can sum finite values an infinite number of times and still arrive at a finite result. Perhaps finite numbers, in a sense, possess an infinite quality beneath the surface.
Hilbert’s Paradox of the Grand Hotel
Infinity can be larger than itself—or perhaps even smaller. Are there various magnitudes of infinity? Consider a hotel with infinitely many rooms filled with guests. If we ask everyone to move to room number twice their current number, we suddenly create an abundance of vacancies!
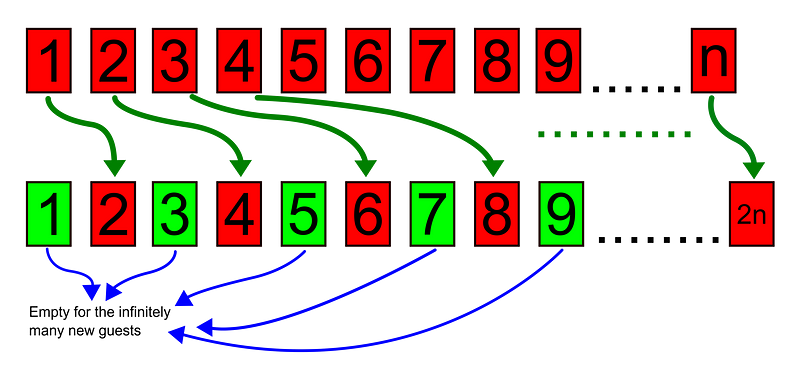
Mathematically, this illustrates the notion that infinity can equal two times infinity, allowing for newly available rooms even though the hotel was previously full.
Conclusion of Philosophical Questions
Can we assert that infinity genuinely exists? Some argue it doesn't; for instance, if infinite mass were real, it would yield infinite gravitational pull, making existence impossible.
“Infinity is merely a practical concept; it cannot be observed in reality,” stated Aristotle, who differentiated between platonic infinity (actual infinity) and potential infinity—the latter being something that can grow endlessly without being fully realized.
An interesting correlation can be made between infinity and concepts of repetition, recursion, and cycles. The ability to replicate processes leads to the notion of infinity, reflecting invariance in mathematical operations. This allows for endless iterations under the same conditions.
The Mathematical Journey Through Infinity
We can frame these philosophical inquiries using mathematics, enabling formal and objective study of infinity.
Series and Summation
A fundamental approach to infinity in mathematics involves infinite summation, known as a series:

The process involves starting from a specific number (n=1) in the summation notation and incrementally adding +1 to n, continuing this until reaching infinity.
There are numerous fascinating series; among my favorites are:
- Geometric Series
- Taylor and Maclaurin Series
- Fourier Series
- Dirichlet Series
- Alternating Series
One of the most renowned series, associated with a $1 million prize, is the Riemann Hypothesis:
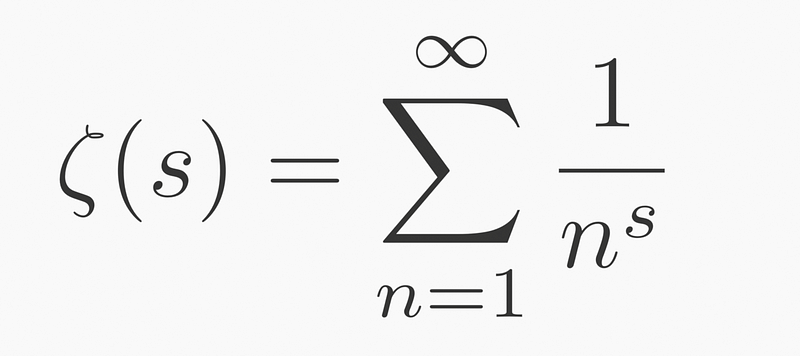
This series acts as a generalization of the others mentioned, signifying that understanding this “ultimate” series grants insight into many related concepts.
Future Explorations
I must pause here, as this topic could expand infinitely. I intend to provide an overview of subsequent subjects in future writings, though they warrant their own dedicated discussions.
Sets and Infinity
In the late 19th century, mathematicians sought to establish a strong foundation for mathematics through rigorous axioms. A key figure in this endeavor was Cantor, who distinguished between countable and uncountable infinities.
Countable infinity refers to sets that can establish a one-to-one correspondence with natural numbers. In contrast, non-countable infinity cannot be matched in this way. For instance, while we can assign numbers to stars in our universe, what happens when we consider other universes?
Cantor also made crucial distinctions between cardinal numbers (reflecting size) and ordinal numbers (which denote order). These concepts paved the way for the development of transfinite numbers, representing initial steps toward grasping infinity.
Gödel’s Incompleteness Theorem
While I won't delve deeply into Gödel's theorem now, it relates closely to infinity. Common interpretations suggest “some truths cannot be proven,” but I contend that only axioms lack proof, and if something is unprovable, it often indicates the need for better axioms.
Infinity remains a central issue in many mathematical explorations, including Turing machines and undecidability, as well as concepts like the halting problem and Russell's paradox.
Calculus and Infinity
With Cantor’s set theory, we gained insights into the nature of infinity. However, calculus enables us to actively work with these concepts. Historically, mathematics primarily focused on finite numbers, but the introduction of series opened pathways to infinity.
Calculus also allows for the inclusion of infinitesimal numbers—values that are almost zero, yet not quite. The summation symbol has evolved to represent this continuous change through the use of 'dx'.

Since Newton's time, calculus has become essential in mathematics, physics, and engineering. Although we often perceive infinity as detached from reality, understanding it—or utilizing it in calculus—enables us to model the world more effectively.
Could it be that our reality is fundamentally rooted in infinity, and that finite numbers are merely illusions?
Singularity in Calculus
An invaluable tool for studying infinity in calculus is the concept of singularity. Unfortunately, many learners do not explore this, as traditional calculus emphasizes real analysis, while singularities are more relevant in complex analysis.
While adding infinitesimal values yields excellent results, encountering a singularity—a point where a function is undefined—poses challenges. However, we have developed methods to navigate these obstacles, particularly concerning poles (a type of singularity).
Could we extend these ideas further, linking singularities to transfinite and p-adic numbers?
Thank you for joining me on this mathematical exploration!