The Enigmatic Nature of Determinants and Pseudovectors
Written on
Chapter 1: Understanding Determinants
In the realm of abstract mathematics, determinants are fascinating constructs that serve as "scalar" functions for square matrices. A succinct yet profound definition describes the determinant as the singular function that is multilinear across the rows (or columns) of a square matrix, acting as a homomorphism from the algebra of square matrices to their corresponding field. This function is not only unique but also surjective. In this context, square matrices correspond to homogeneous linear operators in an N-dimensional vector space.
The Allure of Determinants
One might initially perceive determinants as mundane, yet my enthusiasm for mathematics is rooted in my understanding of them. This definition, while elegant, sometimes requires an alternative approach—one that, although logically equivalent, is less concise and can facilitate proof and comprehension.
In the framework of Clifford Algebras, the determinant is categorized as a pseudoscalar. It represents the highest-grade element in the algebra, commuting with all other elements similarly to a scalar. However, unlike a scalar, the determinant undergoes transformations during coordinate changes, akin to the Levi-Civita symbol.
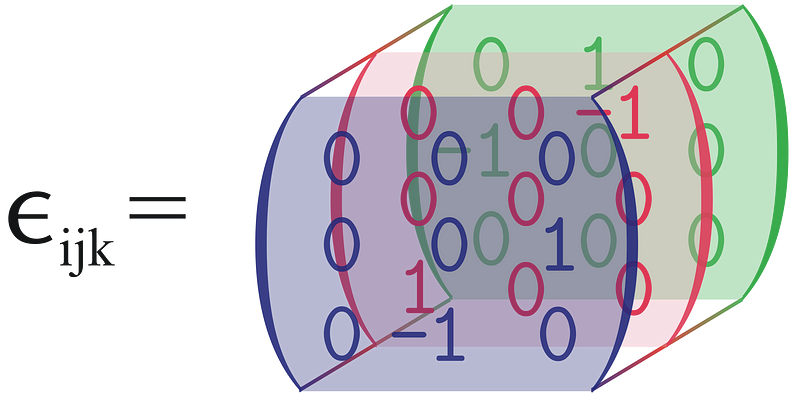
The determinant, viewed as a multilinear function of vectors (the matrix rows) in an N-dimensional space, embodies the Levi-Civita symbol. By definition, the Levi-Civita symbol is the unique alternating, multilinear function of N vectors, with a value of one for the standard basis of N-dimensional space corresponding to the identity matrix.
The geometric interpretation of the determinant reveals it as the signed hypervolume of the parallelepiped formed by the vectors represented by the matrix rows. The magnitude corresponds to the conventional volume, while the sign, dictated by the permutation of the vectors, introduces a notion of chirality—designating a vector basis as either left or right. This sign also enables the classification of permutations as either even or odd, making the determinant a parity detection mechanism. For any N-dimensional vector space, it accepts N vector inputs and yields either a positive (right) or negative (left) sign. It’s essential to clarify that “right” and “left” are mere conventions, devoid of moral implications.
Reflections across any basis vector result in an alternation—essentially a swap of vectors, thereby altering the sign of the determinant. This leads to the consideration of the vector basis as belonging to a root system, a topic for another discussion. While the determinant behaves like a tensor in various respects, it is not entirely a tensor; it exhibits a pseudo-tensor characteristic, reflecting an anomalous sign flip during reflections, similar to a magnetic field.
The first video titled "A Strange Determinant" delves into the unusual properties of determinants, providing visual insights into their mathematical significance.
The determinant in N-dimensional space, once normalized, stands as the unique totally antisymmetric rank N tensor—a definition consistent with our earlier description.
Chapter 2: The Levi-Civita Symbol and Its Applications
The Levi-Civita symbol, a fundamental element in mathematics—especially in linear algebra, tensor analysis, and differential geometry—is vital for understanding how determinants function.
The second video, "Pseudoscalar," explores the intricacies of pseudoscalars and their role in mathematical contexts, shedding light on their importance.
The relationship between the determinant and the Levi-Civita symbol becomes evident in three dimensions, where each component of epsilon correlates to an antisymmetric matrix that represents a component of a magnetic field. The operation of multiplying a tensor by epsilon is analogous to the Hodge dual; for instance, the vector (Bx, By, Bz) transforms into an antisymmetric two-form, the most natural representation of a magnetic field.
The “Anomalous” Sign Flip of Pseudovectors in Electromagnetism
While it is perfectly acceptable to depict a magnetic field as a vector, it is essential to recognize that this perspective, known as the Hodge dual, is most effective in three dimensions. In four dimensions, for example, the Hodge dual of a two-form remains another two-form, making this approach less intuitive in higher dimensions. However, many problems can be effectively addressed within the confines of three-dimensional space.
We inhabit a three-dimensional world, and this dimensionality is unlikely to change unexpectedly. Thus, any strategy that enhances visualization and aids in accurately predicting natural phenomena is valid. Dismissing simpler methods for more complex theories is unnecessary, particularly when straightforward solutions suffice.
Unless you’re named Alice, there’s little risk of traversing a mirror that whimsically alters the parity of your macroscopic universe anytime soon!