A Beginner's Guide to Functions and Continuity in Calculus
Written on
Chapter 1: Introduction to Calculus
This article marks the beginning of a series aimed at demystifying calculus for beginners. The journey starts from the very basics to build a comprehensive understanding.
Calculus often appears daunting to many because it represents a significant transition from basic algebra and arithmetic to the realm of function theory. However, with a little patience and focus on foundational concepts, it can reveal itself as a fascinating and practical area of study.
Upon my initial exploration of calculus, I felt a surge of excitement; prior to that moment, mathematics had seemed mundane to me. I was ready to move past simple equations and transformations, and then I encountered derivatives, igniting my interest.
Calculus is an essential tool for solving complex problems that cannot be tackled using basic arithmetic alone. It can feel almost magical as you navigate through problems, guided by the right questions until you arrive at a solution. Yet, understanding the underlying principles is crucial for deeper comprehension.
Sets in Mathematics
In mathematics, sets serve as foundational objects. While the true nature of a set is a complex topic, we can start by considering them as collections of elements. Examples include number sets like whole numbers and real numbers, as well as finite sets such as {1, 2, 3}.
The notation ( a in A ) indicates that an element ( a ) belongs to set ( A ). A subset ( A ) of set ( B ) is expressed as ( A subseteq B ), meaning that every element ( x ) in ( A ) is also in ( B ) (i.e., if ( x in A ), then ( x in B )). For instance, {1, 3} is a subset of {1, 2, 3}.
In our calculus discussions, we will focus on functions of real or complex numbers. Unless otherwise specified, we will assume these functions map from subsets of real numbers to real numbers. While complex numbers will feature later on, we will address them as they become relevant.
Understanding Functions
Calculus is fundamentally about functions. It’s essential to grasp the concept of functions before proceeding further. Instead of delving into a set-theoretic definition, we will approach functions intuitively.
A function ( f ) is associated with two critical sets: the domain and the codomain. You can think of ( f ) as a rule that takes an input from the domain and produces exactly one output in the codomain. If we denote the domain as ( A ) and the codomain as ( B ), we can succinctly represent this as ( f: A to B ).
For example, the function ( f: mathbb{R} to mathbb{R} ) defined by ( f(x) = 2x ) illustrates this concept.
Continuous Functions
Functions can exhibit a diverse array of properties. In calculus, we generally work with continuous functions. Informally, a function is considered continuous if its graph does not have any abrupt jumps; rather, it appears as a connected curve.
A function is said to be discontinuous at a point ( a ) if there is a jump in the graph at that location.

An illustrative case is the function ( f(x) = 1/x ), which has a discontinuity at ( x=0 ). In this scenario, there is no finite distance between the "ends" of the graph, underscoring the importance of understanding continuity.
What Is Continuity, Really?
While I’ve provided an intuitive understanding of continuity, you may wish to delve deeper into formal definitions, such as those involving delta-epsilon criteria.
Consider a function ( f: A to B ). The continuity of ( f ) means that for every ( a in A ):
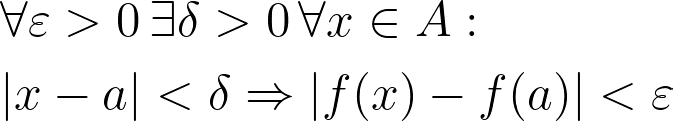
For those unfamiliar with mathematical logic, this notation expresses that for any value ( a ) in the domain ( A ), you can find a number ( delta ) such that if ( x ) is within ( delta ) of ( a ), then the distance between ( f(a) ) and ( f(x) ) is less than any specified ( epsilon ).
Although this might seem complex, don’t worry if you don’t grasp it fully. You will learn calculus effectively without needing to understand every detail of this definition.
Another useful perspective on continuity is that the limit of the function value as the input approaches a number ( a ) from the left must equal the limit as it approaches from the right:
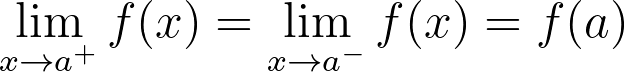
This can be expressed as:

This notation is valid only if the limit exists, which occurs when approaching the same value from both directions.
In this brief introductory article, we’ve laid the groundwork for our next discussion on limits.
The first video titled "1.5 Functions and Continuity" provides a visual overview of these concepts and will help deepen your understanding.
The second video, "3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus," further elaborates on continuity and related concepts.
See you in the next article!