Chapter 1: Introduction to Archimedes

Eric Temple Bell, a renowned mathematician, once highlighted the significance of Archimedes in his popular book, "Men of Mathematics." He stated that among the three most influential mathematicians in history, Archimedes is often cited alongside Newton and Gauss. Given the context of their respective eras, many argue that Archimedes deserves the top spot.

Chapter 2: Who Was Archimedes?

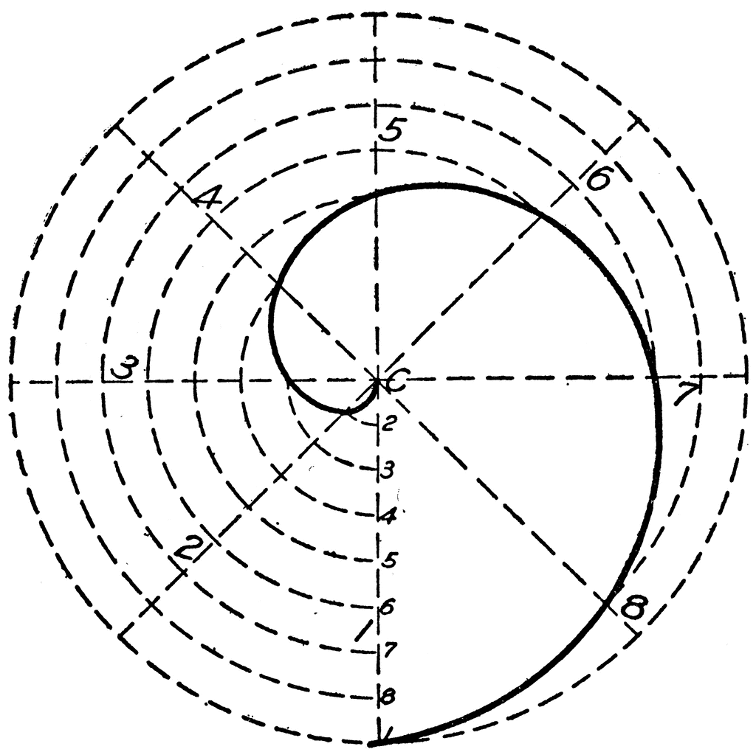
Archimedes (287–212 BC) was a Greek mathematician, physicist, engineer, inventor, and astronomer, recognized as one of history's greatest mathematical minds. His notable contributions include the anticipation of modern analytical methods and calculus, an approximation of π, the study of the Archimedean spiral with practical applications, as well as foundational work in hydrostatics and statics, including the lever principle. He was among the first to use mathematics to explore physical phenomena.

Chapter 3: The Legacy of Democritus

Democritus, a pre-Socratic philosopher known for his atomic theory, was also a notable mathematician. Although none of his numerous works (over 75 titles) survive, he made significant contributions to mathematics, including the understanding that a cone and pyramid with identical bases and heights have one-third the volume of a cylinder or prism.

Chapter 4: The Greeks and Analytic Geometry

Though the formal concept of analytic geometry was introduced by René Descartes in the 1600s, the Greeks had already laid foundational ideas for it. They recognized that in a plane, one could analyze loci using distances to two perpendicular lines, leading to the concept of circles.

Chapter 5: Archimedes and the Sphere's Volume

Archimedes was pioneering in applying mathematical techniques to the field of physics, famously stating, "Give me a place to stand, and with a lever, I will move the whole world."

To illustrate Archimedes' genius, consider the following circle, as shown in Figure 6.

By revolving this circle around its diameter, a sphere is formed. The formulas representing the areas of the cone and cylinder formed during this revolution are as follows:

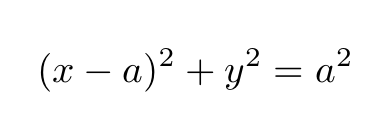
When we multiply the area of the circle by 2a, we can derive further insights into the volume relationships involved.

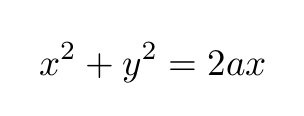
Rearranging the geometric figures, Archimedes ingeniously applied the law of the lever to demonstrate the volume relationships among the sphere, cone, and cylinder.

By employing Democritus' theorem about the volume of a cone, Archimedes concluded that:

This groundbreaking result showcases Archimedes' extraordinary intellect, as noted by mathematician George F. Simmons: "The ideas discussed in this derivation were created by a man who has been described — with good reason — as 'the greatest genius of the ancient world.'"

In this video, "Absolute Genius | Archimedes | S1E1," we delve deeper into Archimedes' life and contributions, further illuminating his monumental impact on mathematics and science.

The second video, "The Life and Legacy of Archimedes: The Genius Mathematician and Inventor," provides insights into Archimedes' enduring influence and legacy in mathematics.

Conclusion

Thank you for exploring the genius of Archimedes! I welcome any constructive feedback or thoughts. For additional resources related to mathematics, physics, data science, and finance, feel free to visit my personal website at www.marcotavora.me.